Norme Euclidienne — Norme (mathématiques) Pour les articles homonymes, voir Norme. En géométrie, la norme est une extension de la valeur absolue des nombres aux vecteurs. Elle permet de mesurer la longueur commune à toutes les représentations d un vecteur dans un… … Wikipédia en Français
Norme euclidienne — Norme (mathématiques) Pour les articles homonymes, voir Norme. En géométrie, la norme est une extension de la valeur absolue des nombres aux vecteurs. Elle permet de mesurer la longueur commune à toutes les représentations d un vecteur dans un… … Wikipédia en Français
Norme d'algèbre — Norme (mathématiques) Pour les articles homonymes, voir Norme. En géométrie, la norme est une extension de la valeur absolue des nombres aux vecteurs. Elle permet de mesurer la longueur commune à toutes les représentations d un vecteur dans un… … Wikipédia en Français
Norme (mathématiques) — Pour les articles homonymes, voir Norme. En géométrie, la norme est une extension de la valeur absolue des nombres aux vecteurs. Elle permet de mesurer la longueur commune à toutes les représentations d un vecteur dans un espace affine, mais… … Wikipédia en Français
euclidienne — ● euclidien, euclidienne adjectif Relatif à Euclide ou à ses travaux. ● euclidien, euclidienne (expressions) adjectif Espace euclidien, espace ponctuel affine muni d une métrique euclidienne, associé à un espace vectoriel euclidien. Géométrie… … Encyclopédie Universelle
Norme d'opérateur — En mathématiques, et plus particulièrement en analyse fonctionnelle, une norme d opérateur ou norme subordonnée est une norme définie sur l espace des opérateurs bornés entre deux espaces vectoriels normés. Entre deux tels espaces, les opérateurs … Wikipédia en Français
Espace vectoriel normé de dimension finie — Topologie d un espace vectoriel de dimension finie En mathématiques, la topologie d un espace vectoriel de dimension finie correspond à un cas particulier d espace vectoriel normé. Cette configuration se produit si la dimension est finie. Elle… … Wikipédia en Français
Distance euclidienne — Distance (mathématiques) Pour les articles homonymes, voir Distance. En mathématiques, une distance est une application qui formalise l idée intuitive de distance, c est à dire la longueur qui sépare deux points. Sommaire 1 Distance sur un… … Wikipédia en Français
Calcul Vectoriel En Géométrie Euclidienne — Cet article traite des opérations portant sur les vecteurs en géométrie euclidienne. Sommaire 1 Opérations sur les vecteurs dans le plan et l espace 1.1 Produit d un vecteur par un scalaire 1.2 Somme de … Wikipédia en Français
Geometrie euclidienne — Géométrie euclidienne Euclide. La géométrie euclidienne commence avec les Éléments d Euclide, qui est à la fois une somme des connaissances géométriques de l époque et une tentative de formalisation mathématique de ces connaissances. Les notions… … Wikipédia en Français
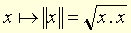 où x.x = f(x,x) est le carré scalaire de x, f étant une forme bilinéaire symétrique non dégénérée positive. (Dans une base orthogonale relativement à f, on a :
où x.x = f(x,x) est le carré scalaire de x, f étant une forme bilinéaire symétrique non dégénérée positive. (Dans une base orthogonale relativement à f, on a : 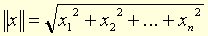 .)
.)